Weighted Graphs

Prerequisites

Introduction to Graphs
Strong and Weak Ties

Outcomes

Know what a weighted graph is and how to construct them using SimpleWeightedGraphs.jl
Implement the shortest path algorithm for traversing a weighted graph

References

Easley and Kleinberg chapter 5 (especially section 5.1-5-3)

# import Pkg; Pkg.add("SimpleWeightedGraphs")

using Graphs, GraphPlot, SimpleWeightedGraphs

Introduction¶

So far we have considered a few types of graphs
- Undirected graph: nodes $A$ and $B$ are connected by an edge
- Directed graph: connection from node $A$ to node $B$
- Strong/weak graphs: each edge is labeled as strong or weak
Today we extend our understanding of networks to talk about weighted graphs
- Each edge is assigned a float denoting the strength of tie
- Ties can be positive (friends) or negative (enemies)
- Can also very in strength (+2.0 better friends than +0.2)

Weighted Adjacency Matrix¶

In a simple (unweighted) graph, we used a matrix of 0’s and 1’s as an adjacency matrix
- A 1 in row i column j marked an edge between i and j (or from i->j for directed)
- A 0 marked lack of an edge

G1 = complete_graph(4)
locs_x = [1, 2, 3, 2.0]
locs_y = [1.0, 0.7, 1, 0]
labels1 = collect('A':'Z')[1:nv(G1)]
gplot(G1, locs_x, locs_y, nodelabel=labels1)

A1 = adjacency_matrix(G1)

4×4 SparseArrays.SparseMatrixCSC{Int64, Int64} with 12 stored entries:
 ⋅  1  1  1
 1  ⋅  1  1
 1  1  ⋅  1
 1  1  1  ⋅

We can extend idea of adjacency matrix to include weighted edges
Suppose nodes A, B, C are friends -- but A-C are best friends
Also suppose that all of A, B, C consider D an enemy
To represent this we might say weight of edges is:
- A-B and B-C: 1.0
- A-C: 2.0
- A-D, B-D, C-D: -1.0
Here’s the adjacency matrix

A2 = [0 1 2 -1; 1 0 1 -1; 2 1 0 -1; -1 -1 -1.0 0]

4×4 Matrix{Float64}:
  0.0   1.0   2.0  -1.0
  1.0   0.0   1.0  -1.0
  2.0   1.0   0.0  -1.0
 -1.0  -1.0  -1.0   0.0

And here is how we might visualize this graph (notice the labeled edges)

G2 = SimpleWeightedGraph(A2)
gplot(
    G2, locs_x, locs_y,
    nodelabel=labels1, edgelabel=weight.(edges(G2)),
)

Shortest Paths¶

We talked previously about shortest paths for a Graph
This was defined as the minimum number of edges needed to move from node n1 to node n2
When we have a weighted graph things get more interesting...
Let $w_{ab}$ represent the weight connecting nodes $A$ and $B$
Define the shortest path between n1 and n2 as the path that minimizes $\sum w_{ab}$ for all edges A->B along a path

Example¶

Consider the following directed graph

A3 = [
    0 1 5 3 0 0 0
    0 0 0 9 6 0 0
    0 0 0 0 0 2 0
    0 0 0 0 0 4 8
    0 0 0 0 0 0 4
    0 0 0 0 0 0 1
    0 0 0 0 0 0 0
]
G3 = SimpleWeightedDiGraph(A3)

#plotting details
locs_x_3 = [3, 5, 1, 3, 4, 2, 3.0]
locs_y_3 = [1, 2, 2, 3, 4, 4, 5.0]
labels3 = collect('A':'Z')[1:size(A3, 1)]
gplot(G3, locs_x_3, locs_y_3, nodelabel=labels3, edgelabel=weight.(edges(G3)))

We wish to travel from node A to node G at minimum cost
The shortest path (ignoring weights) is A-D-G
Taking into account weights we have 3 + 8 = 11
There are two other paths that lead to lower cost (total of 8)
- A-C-F-G has cost 5 + 2 + 1 = 8
- A-D-F-G has cost 3 + 4 + 1 = 8
For this small graph, we could find these paths by hand
For a larger one, we will need an algorithm...

Shortest path algorithm¶

Let $J(v)$ be the minimum cost-to-go from node $v$ to node G
Suppose that we know $J(v)$ for each node $v$ , as shown below for our example graph
- Note $J(G) = 0$

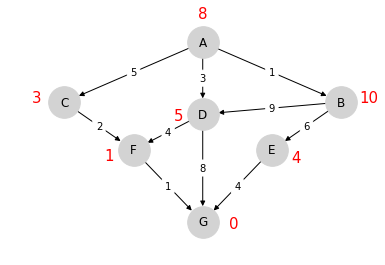
https://compsosci-resources.s3.amazonaws.com/graph-theory-lectures/images/graph_costs.png

With $J(v)$ in hand, the following algorithm will find the cost-minimizing path from $A$ to $G$ :
1. Start with $v = A$
2. From current node $v$ move to any node that solves $\min_{n \in F_v} w_{vn} + J(n)$ , where $F_v$ is the set of nodes that can be reached from $v$ .
3. Update notation to set $v = n$
4. Repeat steps 2-3 (making note of which we visit) until $v = G$

Exercise: Traversing Cost-Minimizing Path¶

Let’s implement the algorithm above
Below I have started a function called traverse_graph
Your task is to complete it until you get that the minimum cost path has a cost of 8 and length(4)

J3 = [8, 10, 3, 5, 4, 1, 0]

7-element Vector{Int64}:
  8
 10
  3
  5
  4
  1
  0

function traverse_graph(
        G::SimpleWeightedDiGraph, 
        J::AbstractArray, 
        start_node::Int, end_node::Int
    )
    path = Int[start_node]
    cost = 0.0
    W = weights(G)

    # TODO: step1, initialize v
    v = 1  # CHANGE ME
    num = 0
    while v != end_node && num < nv(G)  # prevent infinite loop
        num +=1
        F_v = neighbors(G, v)

        # TODO: step 2, compute costs for all n in F_v
        costs = [0 for n in F_v]  # CHANGE ME

        n = F_v[argmin(costs)]

        # TODO: how should we update cost?
        cost += 0   # CHANGE ME

        push!(path, n)

        # TODO: step 3 -- update v
        v = v  # CHANGE ME
    end
    path, cost
end

traverse_graph (generic function with 1 method)

traverse_graph(G3, J3, 1, 7)

([1, 2, 2, 2, 2, 2, 2, 2], 0.0)

But what about $J(v)$ ¶

The shortest path algorithm we presented above sounds simple, but assumed we know $J(v)$
How can we find it?
If you stare at the following equation long enough, you’ll be convinced that $J$ satisfies
$J(v) = \min_{n \in F_v} w_{vn} + J(n)$
(1)
This is known as the Bellman equation
It is a restriction that $J$ must satisfy
We’ll use this restriction to compute $J$

Computing J: Guess and Iterate¶

We’ll present the standard algorithm for computing $J(v)$
This is an iterative method
Let $i$ represent the iteration we are on and $J_i(v)$ be the guess for $J(v)$ on iteration $i$
Algorithm
1. Set $i=0$ , and $J_i(v) = 0 \forall v$
2. Set $J_{i+1}(v) = \min_{n \in F_v} w_{vn} + J_i(n) \forall n$
3. Check if $J_{i+1}$ and $J_i$ are equal for all $v$ -- if not set $i = i+1$ and see repeat steps 2-3
This algorithm converges to $J$ (we won’t prove it here...)

Implementation¶

Let’s now implement the algorithm!
We’ll walk you through our implementation

cost(W, J, n, v) = W[v, n] + J[n]

cost (generic function with 1 method)

function compute_J(G::SimpleWeightedDiGraph, dest_node::Int)
    N = nv(G)
    # step 1. start with zeros
    i = 0
    Ji = zeros(N)

    next_J = zeros(N)

    W = weights(G)

    done = false
    while !done
        i += 1
        for v in 1:N
            if v == dest_node
                next_J[v] = 0
                continue
            end
            F_v = neighbors(G, v)
            costs = [cost(W, Ji, n, v) for n in F_v]
            next_J[v] = minimum(costs)
        end
        done = all(next_J .≈ Ji)
        copy!(Ji, next_J)
    end
    Ji
end

compute_J (generic function with 1 method)

compute_J(G3, 7)

7-element Vector{Float64}:
  8.0
 10.0
  3.0
  5.0
  4.0
  1.0
  0.0

Exercise: Shortest Path¶

Let’s now combine the two functions to compute a shortest path (and associated cost) for a graph
Your task is to fill in the function below and get the test to pass

"""
Given a weighted graph `G`, enumerate a shortest path between `start_node` and `end_node`
"""
function shortest_path(G::SimpleWeightedDiGraph, start_node::Int, end_node::Int)
    # your code here
end

shortest_path

Summary¶

Weighted graphs allow us to analyze the cost of travsersing paths
- Applied in situations like traffic flows (on physical roads/bridges), resource planning, supply chain, international trade (weights as tarrifs), and more
Programming skills...
- We built up an algorithm shortest_path using two smaller routines: traverse_graph, compute_J
- For each of the 3 functions we were able to write tests to verify code correctness
- Good habit to break a hard problem into smaller sub-problems that can be implemented/tested separately
- Then compose overall routine using functions for sub-problems
- Not all practitioners do this... we’ve seen some scary notebooks and scripts... don’t do that... you know better

Graph Theory 2

Homophily