Structural Balance

Prerequisites

• Introduction to Graphs
• Strong and Weak Ties
• Weighted Graphs

Outcomes

• Understand the structural balance property for sets of three nodes
• Understand the structural balance theorem for a graph
• Recognize structural balance in a weighted graph

References

• Easley and Kleinberg chapter 5 (especially section 5.1-5-3)

Introduction¶

• We now shift our discussion to the notion of whether or not a network is balanced
• For this discussion we will use weighted graphs, where weights are one of
  • 1: if nodes are friends (also called +)
  • 0: if they don’t know eachother
  • -1: if nodes are enemies (also called -)
• We won’t consider strength of ties right now
• We will also limit discussion to complete graphs (cliques) where all nodes are connected to all other nodes

Balance in Triangles¶

• To start thinking about balance, consider the possible configurations of + and - edges in a triangle
• There are 4 options as shown below

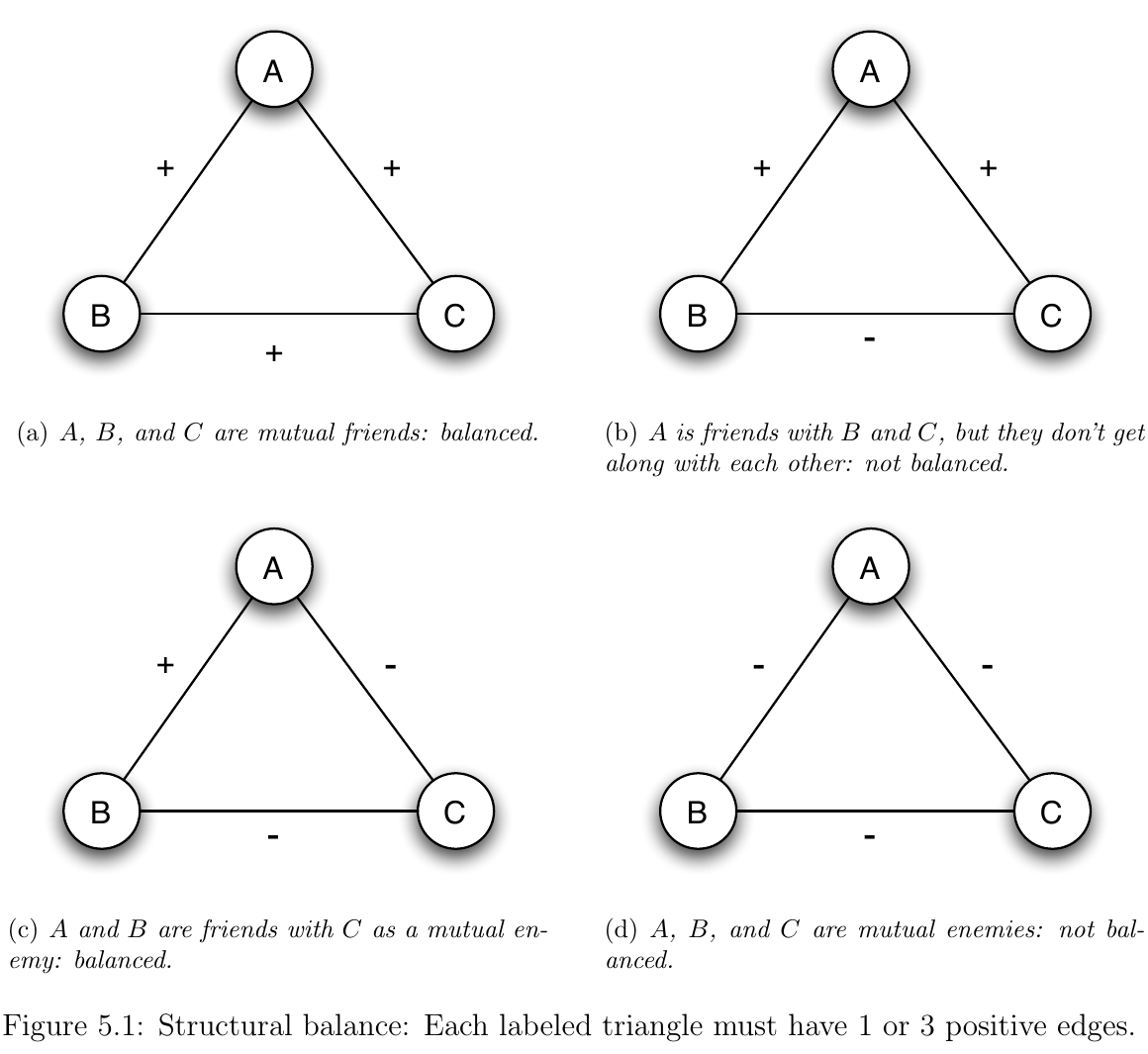
• In (a) all people are friends -- this is happy and balanced
• In (c) A-B are friends with a common enemy C -- nobody has reason to change alliances => balanced
• In (b) A is friends with B and C, but they are enemies -- B and C may try to flip A against other => not balanced
• In (d) all are enemies -- two parties have incentive to team up against common enemy => not balanced

Balance In Graphs¶

• This definition of balance in triangles can be extended to graphs
• A complete graph G satisfies the Structural Balance Property if for every set of three nodes, exactly one or three of the edges is labeled +

Implications: Balance Theorem¶

• One implication of the Structural Balance Property is the Balance Theorem

If a labeled complete graph is balanced, then either all pairs of nodes are friends, or else the nodes can be divided into two groups, X and Y , such that every pair of nodes in X like each other, every pair of nodes in Y like each other, and everyone in X is the enemy of everyone in Y .

• Notice the strength of the statement: either all + or two mutually exclusive groups of friends that are all enemies with other group

Proving Balance Theorem¶

• We will provide some intuition for how to prove the Balance Theorem, which will help us understand why it is true
• Consider a complete Graph G
• Two alternative cases:
  1. Everyone is friends: satisfies theorem by definition
  2. There are some + and some - edges: need to prove
• For case 2, we must be able to split G into $X$ and $Y$ where the following hold
  1. Every node in $X$ is friends with every other node in $X$
  2. Every node in $Y$ is friends with every other node in $Y$
  3. Every node in $X$ is enemies with every node in $Y$

Proof by construction¶

• Start with complete, balanced graph $G$ (our only assumption!)
• We will prove the balance theorem by constructing sets $X$ and $Y$ and verifying that the members of these sets satisfy the 3 properties outlined above
• To start, pick any node $A \in G$
• Divide all other nodes that are friends with $A$ into $X$ and enemies into $Y$
• Because $G$ is complete, this is all nodes

Condition 1: $\forall B, C \in X \quad B \rightarrow C = +$¶

• Let $B, C \in X$
• We know $A \rightarrow B = +$ and $A \rightarrow C = +$
• Because graph is balanced, this triangle must have 1 or 3 +
• There are already 2, so it must be that $B \rightarrow C = +$
• B, C were arbitrary, so this part is proven

Condition 2: $\forall D, E \in Y \quad D \rightarrow E = +$¶

• Let $D, E \in Y$
• We know $A \rightarrow D = -$ and $A \rightarrow E = -$
• Because graph is balanced, this triangle must have 1 or 3 +
• There no + and only one option left, so it must be that $D \rightarrow E = +$
• D, E were arbitrary, so this part is proven

Condition 3: $\forall B \in X$ and $E \in Y \quad B \rightarrow E = -$¶

• Let $B \in X$ and $D \in Y$
• We know $A \rightarrow D = -$ and $A \rightarrow B = +$
• Because graph is balanced, this triangle must have 1 or 3 +
• There is one + ($A \rightarrow B$) and only one option left, so it must be that $B \rightarrow D = -$
• B, D were arbitrary, so this part is proven

Summary¶

• We’ve just proven that for any complete, balanced graph $G$; we can partition $G$ into sets $X$ and $Y$ that satisfy the group structure of all friends or two groups of friends
• This has interesting implications for fields like social interactions, international relations, and online behavior

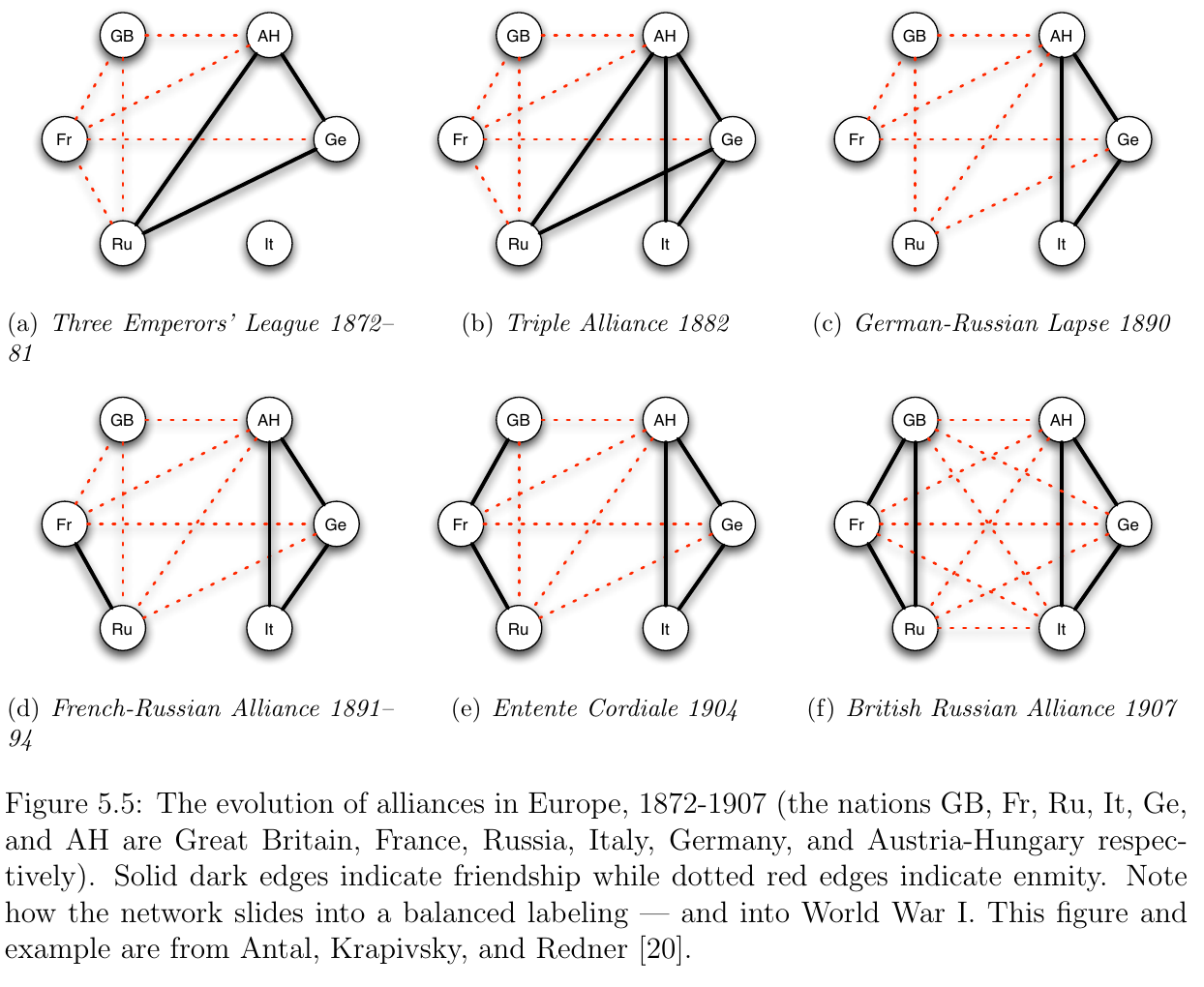
Application: International Relations¶

• Consider the evolution of alliances in Europe between 1872 and 1907 as represented in the graphs below